FA、マシンビジョンで必要とされるテレセントリックレンズ

１．テレセントリックレンズとは？

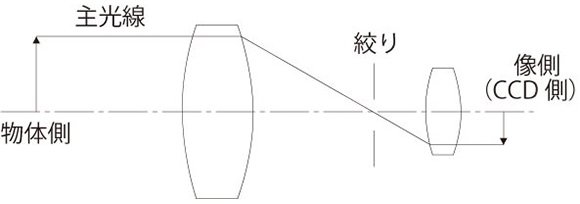
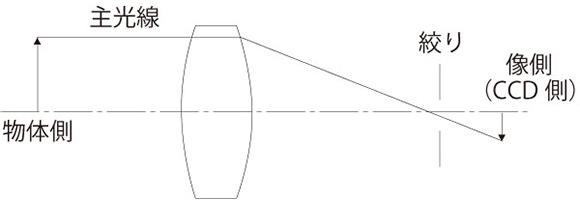
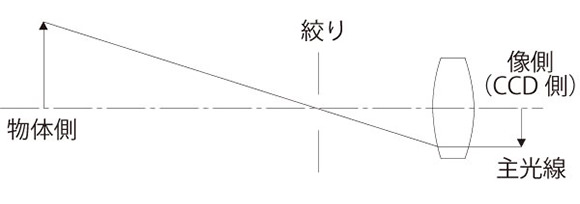
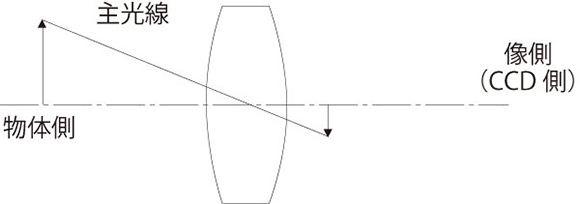
開口絞りがレンズの焦点位置にあるレンズをテレセントリック光学系といいます。開口絞りがレンズの焦点位置にあるので主光線がレンズ光軸に対し物体側、像側、もしくは両側で平行（画角0°）になります。特に物体側と両側テレセントリックレンズは、この画角（テレセントリシティー）が限りなく0°に近いためそのレンズの被写界深度（ピントが合う）の範囲では像の寸法変動がありません。たとえワークが被写界深度から外れピントがボケても画像処理計測が可能な範囲であればこの性能が維持されます。また、同軸落射照明を内蔵する光学系はテレセントリック光学系にするのが理想的です。

１−１．テレセントリックレンズの種類

テレセントリックレンズには両側、物体側、像側の3種類が存在します。下記にそれぞれの特長を記します。

両側テレセントリックレンズ

当社の両側テレセントリックレンズはこちら

物体側テレセントリックレンズ

当社の物体側テレセントリックレンズはこちら

像側テレセントリックレンズ

通常のレンズ

１−２．両側テレセントリックレンズの最大の特長

倍率を変えずにW.D.を変化させることができます。ある一定の倍率を持った有限系のマクロレンズ（非テレセン系）はW.D.を変化させると、それに伴い倍率も変化します。それは物体側テレセントリックレンズも同じです。W.D.を長くすると倍率は低く、W.D.を短くすると倍率は高く変化します。装置の物理的制約のため、倍率を一定のままW.D.を変化させたい場合に、唯一対応できる光学系が両側テレセントリックレンズなのです。

※W.D.の変化量が大きいとディストーション及び解像力が劣化します。ご注意ください。

１−３．テレセントリックレンズの被写界深度

一般的にレンズの絞りを小さくすれば被写界深度は深くなります。しかし、その分有効F値が暗くなり光学的分解能も悪くなります。当社製品のテレセントリックレンズの場合、可変絞りが付いている両側テレセントリックレンズはこれを可変する事によりより深い被写界深度が得られます。また固定絞りの場合はカスタム仕様にて対応させていただきます。

２．テレセントリックレンズと一般マクロ（拡大系）レンズとの違い

テレセントリックレンズは前述したように被写界深度内で被写体寸法は変化しません。それは主光線が光軸に対し0°であるとの理由からです。それに対し一般マクロレンズは主光線が光軸に対し画角を持っています。したがって、その被写界深度内での被写体寸法は画角によって変化します。一般的にコスト面とサイズでは、一般マクロレンズのほうがテレセントリックレンズより安価でコンパクトです。

２−１．画像計測に有利なテレセントリックレンズ

画像計測する場合、レンズと被写体とのW.D.が一定で変化しなければ一般マクロレンズでも問題がありませんが、多少でも変化する場合はテレセントリックレンズでないと計測値にバラつきができます。また、被写体が鏡面の場合は同軸落射照明が内蔵されたテレセントリックレンズを使用するのが理想的です。

２−２．照明方式によるテレセントリックレンズと一般マクロレンズの使い分け

ウエハーなど鏡面の被写体の表面パターン認識の場合は、同軸落射照明が必要です。従ってテレセントリックレンズが主に使われます。平面でも鉄などの金属や樹脂など鏡面でない被写体や実装基板などのアライメント用照明はリングライトや斜めから照射する照明方式が多いので、テレセントリックレンズ以外で一般マクロレンズも使用されます。エッジ検出などの場合は透過照明方式です。照明はハロゲンランプやLED、メタルハライド光源などがあり、波長も一般的な白色光から紫外線、青色、赤色、赤外線などカメラやレンズ系の分光感度特性に合わせて最適な色を選定します。

２−３．テレセントリックレンズと一般マクロレンズの被写界深度の違い

一般マクロレンズと同様にテレセントリックレンズも被写界深度は基本的に深くはありません。それはテレセントリックレンズも一般マクロレンズも被写界深度の求め方（公式）は同じだからです。ただし、前述したように一般マクロレンズの場合は被写界深度内で被写体寸法は変動しますが、テレセントリックレンズは変動しません。

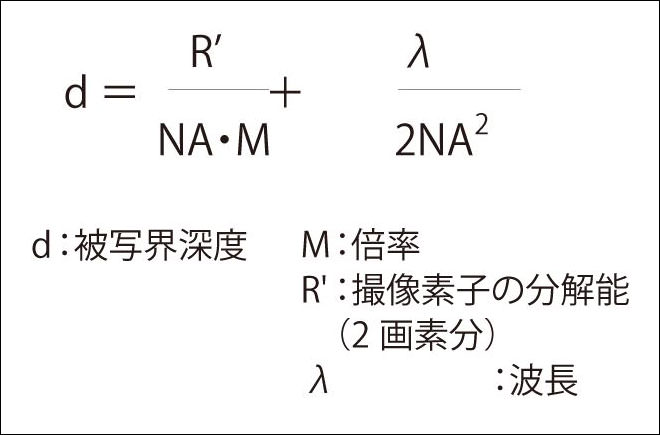
３．被写界深度

３−１．被写界深度に対する当社の考え方

5Mカメラなどの登場で現在のFAカメラのピクセルサイズは益々高精細化になっています。それに伴いレンズもカメラのピクセルサイズに合わせ高N.A.化（=高解像力化）に対応するようになりました。しかしここで最近国内外のユーザーから「色々なレンズメーカーのカタログを見るが高N.A.対応レンズなのに何故スペック上でレンズの被写界深度が深いのか？」といったご質問を受けます。理由は被写界深度を求める数式が各社によって異なるからです。被写界深度の深い表示のメーカーはメガピクセルに関係なく以下の数式を使用しています。

許容錯乱円÷(N.A.×光学倍率)または2{許容錯乱円×実効F値÷(光学倍率)²}

そしてカメラのピクセルサイズに相当する許容錯乱円に40μまたは20μの数値を入れています。
例えば、2/3″5メガピクセルカメラ使用を前提とした場合、1ピクセルサイズは3.45μです。ただし1ピクセルでは白黒判定が出来ないので2ピクセル分として6.9μの数値を入れるべきところを40μまたは20μを入れるのです。この3つの異なる数値を上記数式で計算した場合、被写界深度（DOF）はどうなるでしょうか。

例）2/3″5Mカメラ対応の　N.A.0.08　倍率×1　レンズの場合

①40μの場合　0.04÷(0.08×1)=0.5mmの被写界深度
②20μの場合　0.02÷(0.08×1)=0.25mmの被写界深度
③6.9μの場合　0.0069÷(0.08×1)=0.08625mmの被写界深度

これだけ被写界深度に差が出てしまいます。また上記数式では使用する光源の波長が反映されていません。従ってOPTARTでは使用する波長域も反映されるように以下の数式を使用しています。

DOF=R”/(N.A.×β)+{λ/(2×N.A.×N.A.)}

R″＝: カメラのピクセルサイズ2個分
ex. 2/3″5Mカメラ素子サイズ3.45μmの場合、代入値は0.0069
β″＝: 倍率
λ＝: 光源の波長
ex. 600nm単一波長の場合、代入値は0.0006
N.A.＝: レンズの物体N.A.

以上の数式で上記例題のレンズを計算すると、
DOF=(0.0069/0.08×1)+(0.0006/2×0.0064)=0.13mmとなります。
0.5mm　0.25mm　0.13mm
さて皆様はこの3つの数値のどれを被写界深度として認識するでしょうか。

３−２．許容錯乱円と被写界深度に対する当社の考え方

銀塩カメラの時代から、被写界深度の算出はレンズの最小錯乱円径40μm（ピントずれによる大きさ）という数字を用いて計算することを踏襲していますが、現在のFAカメラのピクセルサイズは小さくなり、その再現能力を鑑みると実勢にそぐいません。例えば1ピクセルサイズ3.45μmの5Mカメラ用いた場合、最小錯乱円は6.9μmに設定しないといけません。当社ではピクセルサイズの効果に光学的効果を加味して、下記の式を用いてよりお客様のご使用環境に近い被写界深度をカタログに記載しています。

DOF=R”/(N.A.×β)+{λ/(2×N.A.×N.A.)}